# 944. 删列造序
力扣原题链接(点我直达) (opens new window)
给定由 N 个小写字母字符串组成的数组 A,其中每个字符串长度相等。
删除 操作的定义是:选出一组要删掉的列,删去 A 中对应列中的所有字符,形式上,第 n 列为 [A[0][n], A[1][n], ..., A[A.length-1][n]])。
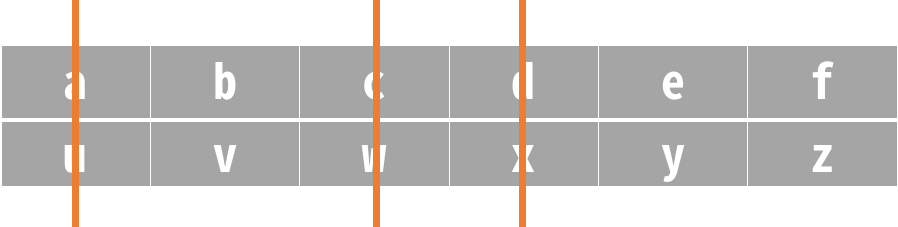
比如,有 A = ["abcdef", "uvwxyz"],

要删掉的列为 {0, 2, 3},删除后 A 为["bef", "vyz"], A 的列分别为["b","v"], ["e","y"], ["f","z"]。
你需要选出一组要删掉的列 D,对 A 执行删除操作,使 A 中剩余的每一列都是 非降序 排列的,然后请你返回 D.length 的最小可能值。
示例 1:
输入:["cba", "daf", "ghi"]
输出:1
解释:
当选择 D = {1},删除后 A 的列为:["c","d","g"] 和 ["a","f","i"],均为非降序排列。
若选择 D = {},那么 A 的列 ["b","a","h"] 就不是非降序排列了。
2
3
4
5
示例 2:
输入:["a", "b"]
输出:0
解释:D = {}
2
3
示例 3:
输入:["zyx", "wvu", "tsr"]
输出:3
解释:D = {0, 1, 2}
2
3
提示:
1 <= A.length <= 1001 <= A[i].length <= 1000
# 第一版,说的很垃圾啊,容易的题目,说的那么难懂
执行用时 :48 ms, 在所有 cpp 提交中击败了89.00%的用户
内存消耗 :13.1 MB, 在所有 cpp 提交中击败了72.99%的用户
int minDeletionSize(vector<string>& A) {
int len1 = A.size(), len2 = A[0].size();
int res=0;
for (int i = 0; i < len2; ++i) {
for (int j = 0; j < len1-1; ++j) {
if (A[j][i] > A[j + 1][i]) {
//cout << A[j][i] << " " << A[j + 1][i] << " j " << j << " i " << i << endl;
res++;
break;
}
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 1029. 两地调度 第一道贪心的题目
力扣原题链接(点我直达) (opens new window)
公司计划面试 2N 人。第 i 人飞往 A 市的费用为 costs[i][0],飞往 B 市的费用为 costs[i][1]。
返回将每个人都飞到某座城市的最低费用,要求每个城市都有 N 人抵达**。**
示例:
输入:[[10,20],[30,200],[400,50],[30,20]]
输出:110
解释:
第一个人去 A 市,费用为 10。
第二个人去 A 市,费用为 30。
第三个人去 B 市,费用为 50。
第四个人去 B 市,费用为 20。
最低总费用为 10 + 30 + 50 + 20 = 110,每个城市都有一半的人在面试。
2
3
4
5
6
7
8
9
提示:
1 <= costs.length <= 100costs.length为偶数1 <= costs[i][0], costs[i][1] <= 1000
# 第一版,看的最优解,挺有道理的
以costs[0]-costs[1]的差值从小到大排列,前一半去A,后一半去B
执行用时 :4 ms, 在所有 cpp 提交中击败了96.28%的用户
内存消耗 :9.3 MB, 在所有 cpp 提交中击败了100.00%的用户
static bool compare(const vector<int>& a,const vector<int>& b) {
return a[0] - a[1] < b[0] - b[1];
}
int twoCitySchedCost(vector<vector<int>>& costs) {
sort(costs.begin(), costs.end(), compare);
int count = 0, sum = 0,len=costs.size();
for (auto& cost : costs) {
if (count * 2 < len) sum += cost[0];
else
sum += cost[1];
count++;
}
return sum;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 1046. 最后一块石头的重量
力扣原题链接(点我直达) (opens new window)
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出两块最重的石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。
提示:
1 <= stones.length <= 301 <= stones[i] <= 1000
# 第一版,优先队列,默认是大顶堆
执行用时 :4 ms, 在所有 cpp 提交中击败了81.08%的用户
内存消耗 :8.3 MB, 在所有 cpp 提交中击败了100.00%的用户
int lastStoneWeight(vector<int>& stones) {
if (stones.size() == 1) return stones[0];
priority_queue<int> res;
int s1, s2;
for (auto& s : stones)
res.push(s);
while (res.size() > 1) {
s1 = res.top();
res.pop();
s2 = res.top();
res.pop();
if (s1 != s2) res.push(s1 - s2);//s1>=s2 所以这里是不需要用abs函数的
}
return res.empty() ? 0 : res.top();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 1049. 最后一块石头的重量 II 好题,真的好题
力扣原题链接(点我直达) (opens new window)
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
示例:
输入:[2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
2
3
4
5
6
7
提示:
1 <= stones.length <= 301 <= stones[i] <= 1000
# 第一版,完全看的思路问题
执行用时 :4 ms, 在所有 cpp 提交中击败了89.93%的用户
内存消耗 :8.6 MB, 在所有 cpp 提交中击败了100.00%的用户
int lastStoneWeightII(vector<int>& stones) {
int sum = accumulate(stones.begin(), stones.end(), 0);
int target = sum / 2;
vector<int> dp = vector<int>(target + 1, 0);
long size = stones.size();
for (int i = 0; i < size; i++) {
int s = stones[i];
for (int j = target; j >= s; j--) {
dp[j] = max(dp[j], dp[j - s] + s);
}
}
return sum - 2 * dp.back();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
等价于最大化半个背包的重量
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sum = accumulate(stones.begin(), stones.end(), 0);
int S = sum / 2;
int N = stones.size();
vector<vector<int> > dp(S + 1, vector<int>(N + 1, 0));
for (int i = 1; i <= S; ++i) {
for (int j = 1; j <= N; ++j) {
dp[i][j] = max(dp[i][j - 1],
(i >= stones[j - 1]) ? dp[i - stones[j - 1]][j - 1] + stones[j - 1] : 0);
}
}
return sum - 2 * dp[S][N];
}
};
// 也可以使用状态压缩后的dp
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sum = accumulate(stones.begin(), stones.end(), 0);
int S = sum / 2;
int N = stones.size();
vector<int> dp(S + 1, 0);
for (int i = 0; i < N; ++i) {
int w = stones[i];
for (int j = S; j >= w; --j) {
dp[j] = max(dp[j], dp[j - w] + w);
}
}
return sum - 2 * dp[S];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 1217. 玩筹码 很无聊的题目
力扣原题链接(点我直达) (opens new window)
数轴上放置了一些筹码,每个筹码的位置存在数组 chips 当中。
你可以对 任何筹码 执行下面两种操作之一(不限操作次数,0 次也可以):
- 将第
i个筹码向左或者右移动 2 个单位,代价为 0。 - 将第
i个筹码向左或者右移动 1 个单位,代价为 1。
最开始的时候,同一位置上也可能放着两个或者更多的筹码。
返回将所有筹码移动到同一位置(任意位置)上所需要的最小代价。
示例 1:
输入:chips = [1,2,3]
输出:1
解释:第二个筹码移动到位置三的代价是 1,第一个筹码移动到位置三的代价是 0,总代价为 1。
2
3
示例 2:
输入:chips = [2,2,2,3,3]
输出:2
解释:第四和第五个筹码移动到位置二的代价都是 1,所以最小总代价为 2。
2
3
提示:
1 <= chips.length <= 1001 <= chips[i] <= 10^9
# 第一版,真的很无聊
执行用时 :4 ms, 在所有 cpp 提交中击败了77.12%的用户
内存消耗 :8.5 MB, 在所有 cpp 提交中击败了100.00%的用户
int minCostToMoveChips(vector<int>& chips) {
int odd = 0, even = 0;
for (auto& elem : chips)
{
if (elem % 2 == 1) {
even++;
}
else {
odd++;
}
}
return min(even, odd);
}
2
3
4
5
6
7
8
9
10
11
12
13
# 1221. 分割平衡字符串
力扣原题链接(点我直达) (opens new window)
在一个「平衡字符串」中,'L' 和 'R' 字符的数量是相同的。
给出一个平衡字符串 s,请你将它分割成尽可能多的平衡字符串。
返回可以通过分割得到的平衡字符串的最大数量。
示例 1:
输入:s = "RLRRLLRLRL"
输出:4
解释:s 可以分割为 "RL", "RRLL", "RL", "RL", 每个子字符串中都包含相同数量的 'L' 和 'R'。
2
3
示例 2:
输入:s = "RLLLLRRRLR"
输出:3
解释:s 可以分割为 "RL", "LLLRRR", "LR", 每个子字符串中都包含相同数量的 'L' 和 'R'。
2
3
示例 3:
输入:s = "LLLLRRRR"
输出:1
解释:s 只能保持原样 "LLLLRRRR".
2
3
提示:
1 <= s.length <= 1000s[i] = 'L' 或 'R'
# 第一版,入门级题目,但是时间太慢
执行用时 :8 ms, 在所有 cpp 提交中击败了8.71%的用户
内存消耗 :8.4 MB, 在所有 cpp 提交中击败了100.00%的用户
int balancedStringSplit(string s) {
//char L = 'L', R = 'R';
int countL = 0, countR = 0,res=0;
for (auto& a : s) {
if (a == 'L') countL++;
else
countR++;
if (countL == countR) {
res++;
countL = 0;
countR = 0;
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 第二版,其实有一步是可以省去的,这样更快一点
执行用时 :4 ms, 在所有 cpp 提交中击败了70.35%的用户
内存消耗 :8.4 MB, 在所有 cpp 提交中击败了100.00%的用户
int balancedStringSplit(string s) {
int countL = 0, countR = 0,res=0;
for (auto& a : s) {
if (a == 'L') countL++;
else
countR++;
if (countL == countR) {
res++;
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
# 第三版,用栈其实也可以,也挺快的
执行用时 :4 ms, 在所有 cpp 提交中击败了70.35%的用户
内存消耗 :8.5 MB, 在所有 cpp 提交中击败了100.00%的用户
int balancedStringSplit(string s) {
int res=0;
stack<char> st;
for (auto& a : s) {
if (st.empty() || a == st.top())
st.push(a);
else
st.pop();
if (st.empty()) ++res;
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
